前向傳播演算法（Forward Propagation）神經網路基礎運算

前向傳播 (Forward Propagation) 是人工神經網路中一個關鍵運算過程。簡單來說，就是將輸入資料從輸入層逐層傳遞到輸出層，並在每一層進行線性轉換和非線性激活的過程。這個過程就像資訊在神經網路中單向流動，最終產生一個預測輸出

前向傳播公式

net_input = Σ(weights * inputs) + bias output = activation_function(net_input)

線性轉換

加權求和

每一個神經元都會將上一層的神經元輸出乘以對應的權重，然後將這些乘積相加，再加上偏置

z = w * x + b

非線性激活

激活函數

為了讓神經網路具有非線性擬合能力，會將線性轉換後的結果輸入到一個激活函數中

• Sigmoid：將輸入值映射到0到1之間
• Tanh：將輸入值映射到-1到1之間
• ReLU：將輸入值映射到0或輸入值本身

a = f(z)

多層網路

由多個層組成的，每一層神經元都與上一層的神經元相連
前向傳播會逐層計算，直到到達輸出層

前向傳播程式碼(Python-NumPy)

import numpy as np

# 假設一個簡單的神經網路，輸入層有2個神經元，隱藏層有3個神經元，輸出層有1個神經元
# 隨機初始化權重和偏置
weights1 = np.random.randn(2, 3)
biases1 = np.random.randn(1, 3)
weights2 = np.random.randn(3, 1)
biases2 = np.random.randn(1, 1)

# 激活函數 (這裡使用ReLU)
def relu(z):
    return np.maximum(0, z)

# 前向傳播
def forward_propagation(X):
    z1 = np.dot(X, weights1) + biases1
    a1 = relu(z1)
    z2 = np.dot(a1, weights2) + biases2
    a2 = relu(z2)
    return a2

# 輸入資料
X = np.array([[1, 2]])

# 進行前向傳播
output = forward_propagation(X)
print(output)

前向傳播的程式碼示例（Python，使用NumPy）
Python
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 假設輸入資料、權重和偏置
inputs = np.array([1, 2, 3])
weights = np.array([[0.2, 0.8, -0.5],
                     [0.5, -0.91, 0.26]])
bias = np.array([0.5, -0.1])

# 前向傳播
net_inputs = np.dot(inputs, weights) + bias
outputs = sigmoid(net_inputs)

print(outputs)

import numpy as np

# 假設輸入資料 X，權重 W，偏置 b，激活函數為 ReLU
def forward_propagation(X, W, b):
    # 計算淨輸入
    net_input = np.dot(X, W) + b
    
    # 應用 ReLU 激活函數
    output = np.maximum(0, net_input)
    
    return output

結論

前向傳播是神經網路訓練基礎。將輸入資料逐層傳遞，最終得到一個預測輸出。這個預測輸出會與真實標籤進行比較，計算出誤差，然後通過反向傳播算法來更新網路的參數

反向傳播演算法（Backpropagation）神經網路學習核心

反向傳播 (Backpropagation) 是一種訓練人工神經網路常見方法。計算損失函數對網路中每個權重的梯度，利用這些梯度來更新權重，以最小化損失，使模型能夠更好地擬合訓練數據

反向傳播就像一個「糾錯」的過程。當神經網路輸出與真實標籤不一致時，反向傳播會將誤差從輸出層逐層傳遞回輸入層，並調整每一層的權重，使得下一次的預測更加準確

反向傳播過程

• 前向傳播： 將輸入資料輸入到神經網路，經過每一層的計算，得到最終的輸出
• 計算損失： 比較神經網路的輸出與真實標籤，計算出損失函數的值
• 反向傳播： 根據損失函數，計算每個權重對損失函數的梯度
• 更新權重： 使用梯度下降法，根據計算出的梯度更新每個權重的值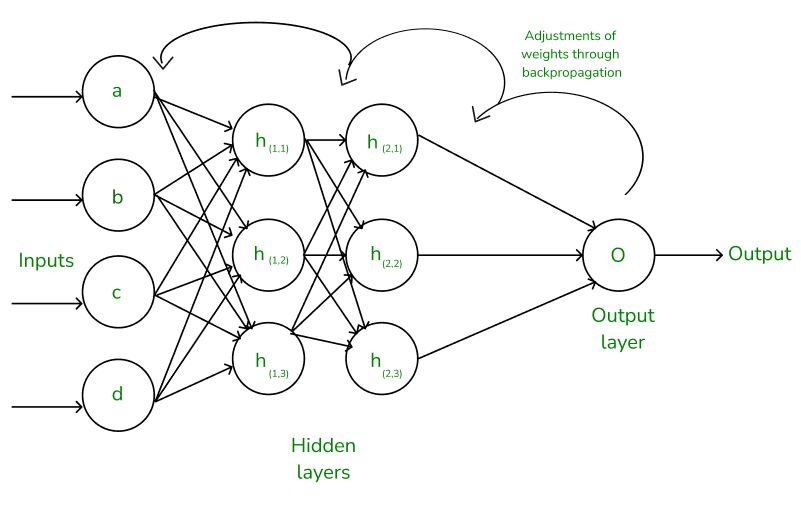
  
  圖片來源:(https://www.geeksforgeeks.org/backpropagation-in-neural-network/)

反向傳播公式

• 損失函數： 常用損失函數有均方誤差 (MSE)、交叉熵損失
• 鏈式法則： 計算複合函數的導數
• 梯度下降法： 更新權重

w = w - learning_rate * gradient

鏈式法則

反向傳播基礎，計算複雜函數的梯度

dL/dw = dL/dz * dz/dw

反向傳播程式碼(Python-NumPy)

import numpy as np

def backpropagation(output, target, weights, bias):
  # 計算誤差
  error = output - target
  
  # 計算輸出層梯度
  delta_output = error * derivative_activation(output)
  
  # ... (計算隐藏層的梯度，更新權重和偏置)
  
  # 更新輸出層的權重和偏置
  weights[-1] -= learning_rate * np.dot(input.T, delta_output)
  bias[-1] -= learning_rate * np.sum(delta_output, axis=0)

反向傳播程式碼(Python-TensorFlow/Keras)

import tensorflow as tf

# 定義模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(10, activation='relu', input_shape=(784,)),
    tf.keras.layers.Dense(10, activation='softmax')
])

# 編譯模型
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 訓練模型
model.fit(x_train, y_train, epochs=10)

為什麼要進行反向傳播？

• 訓練神經網路：訓練神經網路關鍵步驟，通過不斷更新權重，使模型能夠更好地擬合訓練資料
• 優化模型：可以幫助我們找到一組最優的權重，使模型的泛化能力更好

結論

反向傳播是神經網路訓練核心算法。通過反向傳播，可以將誤差信息傳遞回神經網路的每一層，並根據誤差的大小來調整權重，讓模型能夠更好地學習到資料中的規律